HD 5514 Research Methods (Fall 2019)

In-Class Acitivity: Analysis of Variance (ANOVA)
In-Class Acitivity: Multiple pairwise-comparison
- Bonferroni and Holm multiple pairwise-comparisons
- Tukey multiple pairwise-comparisons
In-Class Acitivity: Planned Constrasts
FYI: Visualize your data using ggpubr
- Bar plots with mean +/- se with jittered points
In-Class Acitivity: Tidyverse
- Computes summary tables using dplyr
Assignment 10 (Week 15)

In-Class Acitivity: Analysis of Variance (ANOVA)

Load Data

We are going to use R.appendix1.data from Personality Project. We will load and print the data.

# 1. Loading
data1 <- read.table("http://personality-project.org/r/datasets/R.appendix1.text", 
    header = TRUE)  #read the data into a table
data1

   Dosage Alertness
1       a        30
2       a        38
3       a        35
4       a        41
5       a        27
6       a        24
7       b        32
8       b        26
9       b        31
10      b        29
11      b        27
12      b        35
13      b        21
14      b        25
15      c        17
16      c        21
17      c        20
18      c        19

# 2. Print
head(data1)

  Dosage Alertness
1      a        30
2      a        38
3      a        35
4      a        41
5      a        27
6      a        24

Check Data Set

Check the number of rows and columns.

# Check the dimension of an object
dim(data1)

[1] 18  2

# Display the internal structure of an R object.
str(data1)

'data.frame':   18 obs. of  2 variables:
 $ Dosage   : Factor w/ 3 levels "a","b","c": 1 1 1 1 1 1 2 2 2 2 ...
 $ Alertness: int  30 38 35 41 27 24 32 26 31 29 ...

# Check the levels
levels(data1$Dosage)

[1] "a" "b" "c"

Visualize your data - Boxplot & Histogram

# par(mar=c(1,1,1,1)) # change figure margins if you encounter error

# Boxplot
boxplot(data1$Alertness)

# Boxplot (Alterness by group)
boxplot(data1$Alertness ~ data1$Dosage)

# Histogram
hist(data1$Alertness)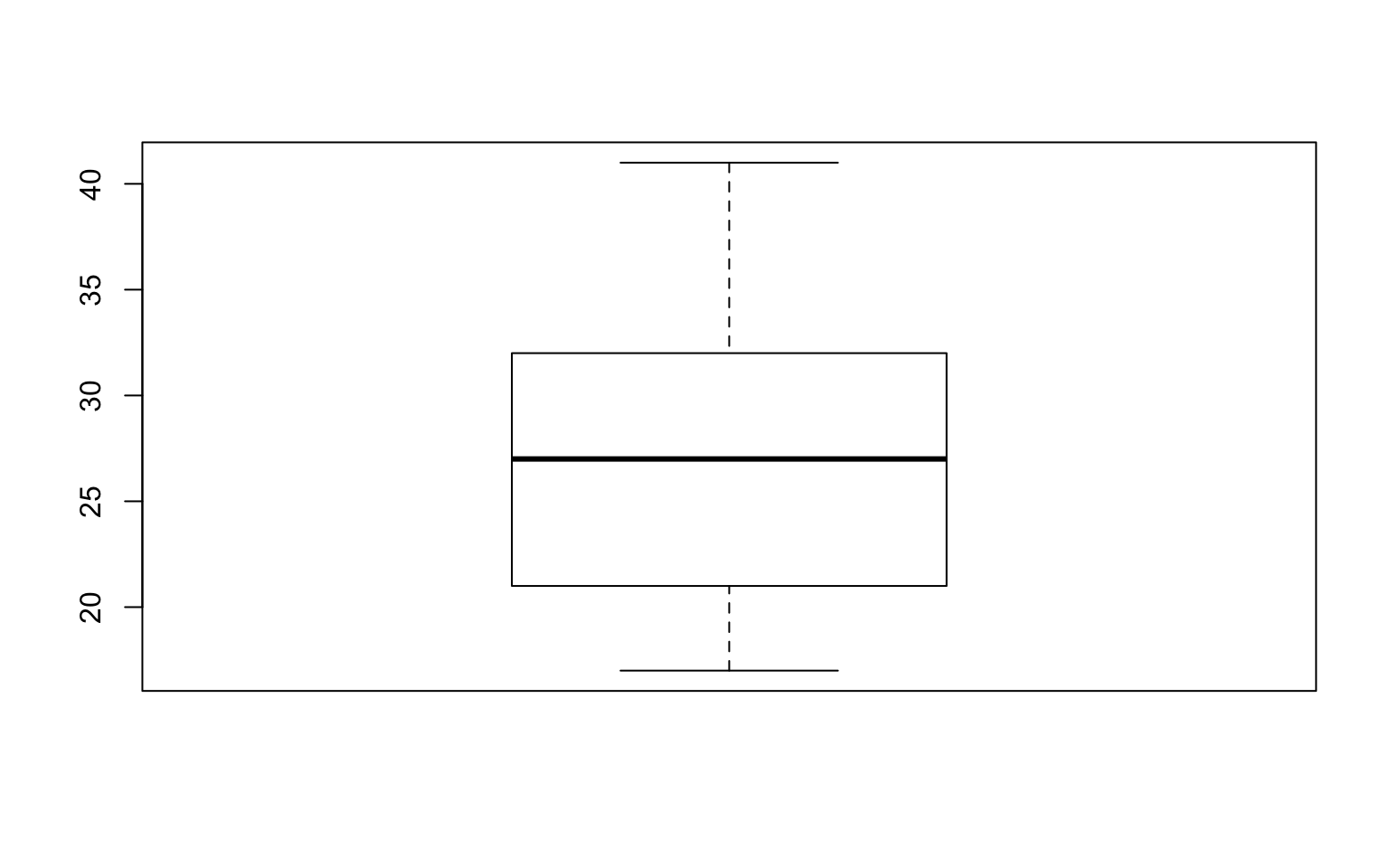

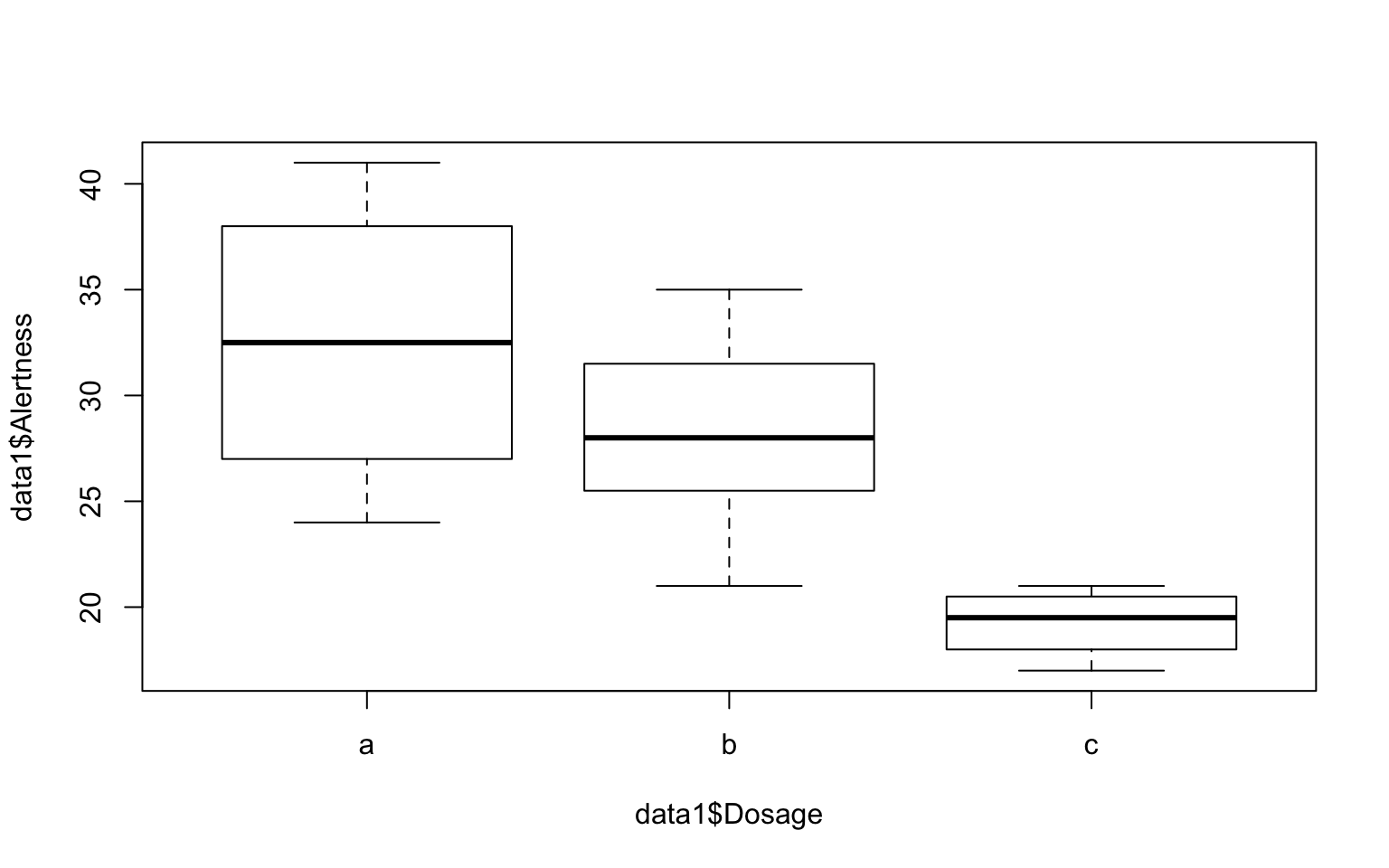
Conduct one-way Anova

# Compute the analysis of variance
aov.ex1 <- aov(Alertness ~ Dosage, data = data1)
# Summary of the analysis
summary(aov.ex1)

            Df Sum Sq Mean Sq F value  Pr(>F)   
Dosage       2  426.2  213.12   8.789 0.00298 **
Residuals   15  363.8   24.25                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Report means

model.tables computes summary tables for model fits, especially aov fits.

# Computes summary table (mean, count)
model.tables(aov.ex1, "means")

Tables of means
Grand mean
         
27.66667 

 Dosage 
       a     b     c
    32.5 28.25 19.25
rep  6.0  8.00  4.00

`?`(model.tables)

Check ANOVA assumptions

ANOVA assumes normal distribution and homogeneity of variances.

Check the homogeneity of variance assumption: Levene’s test

Perform Leven’s test using the function leveneTest in car package. If variance across groups is not significantly different, we can assume the homogeneity of variances in the different groups.

library(car)
leveneTest(Alertness ~ Dosage, data = data1)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value  Pr(>F)  
group  2  4.1667 0.03638 *
      15                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ANOVA test with no assumption of equal variances: Welch one-way test

Welch one-way test is an alternative that does not require thae homogeneity of variance assumption.

oneway.test(Alertness ~ Dosage, data = data1)


    One-way analysis of means (not assuming equal variances)

data:  Alertness and Dosage
F = 19.339, num df = 2.0000, denom df = 9.2651, p-value =
0.0004931

Check the normality assumption

We can assume normality if all the points fall approximately along this reference line. Or you can conduct Shapiro-Wilk test on ANOVA residuals.

# create a normal QQ plot and add a reference line (Run the two lines at the
# same time)
qqnorm(cars$dist)
qqline(cars$dist)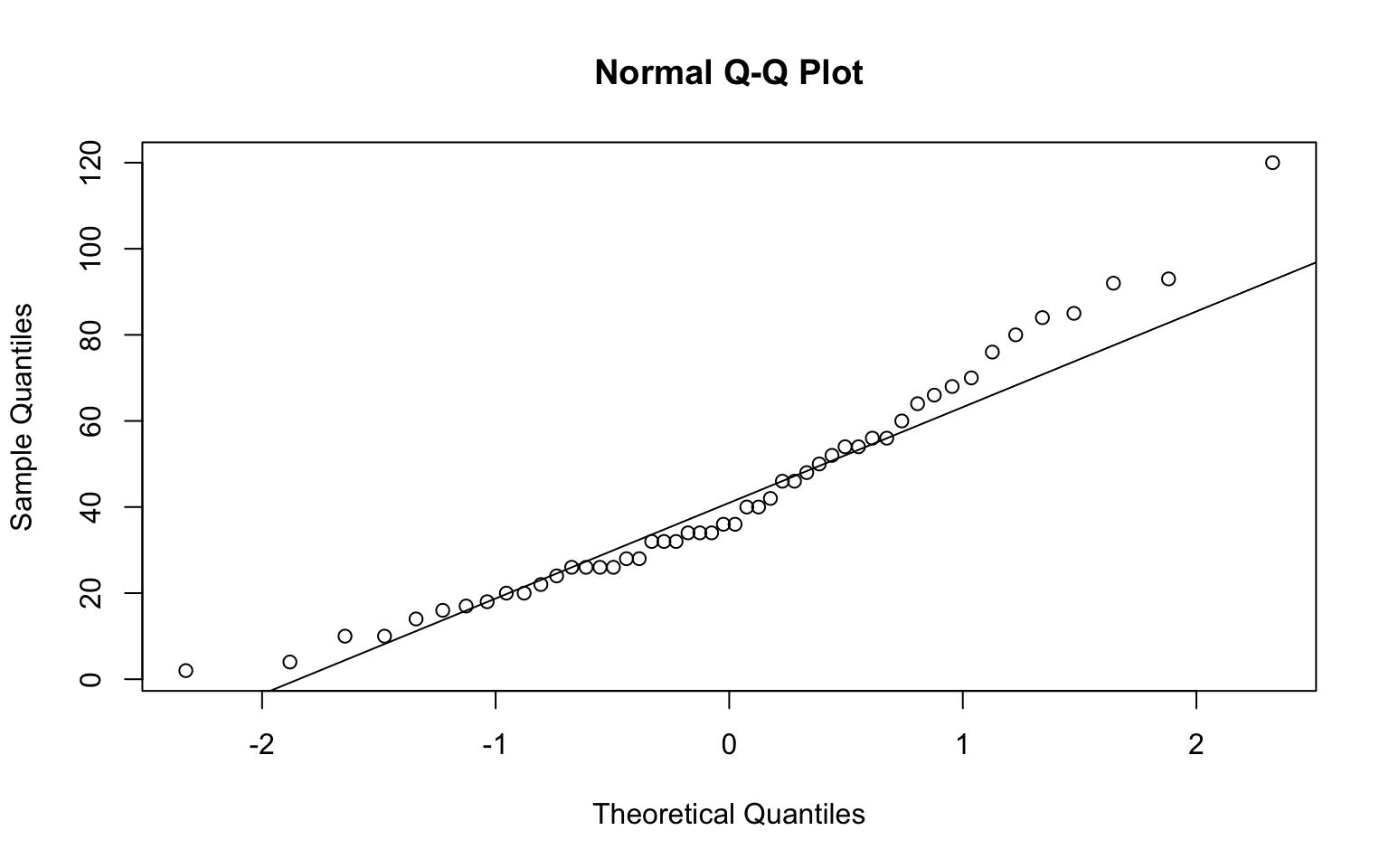

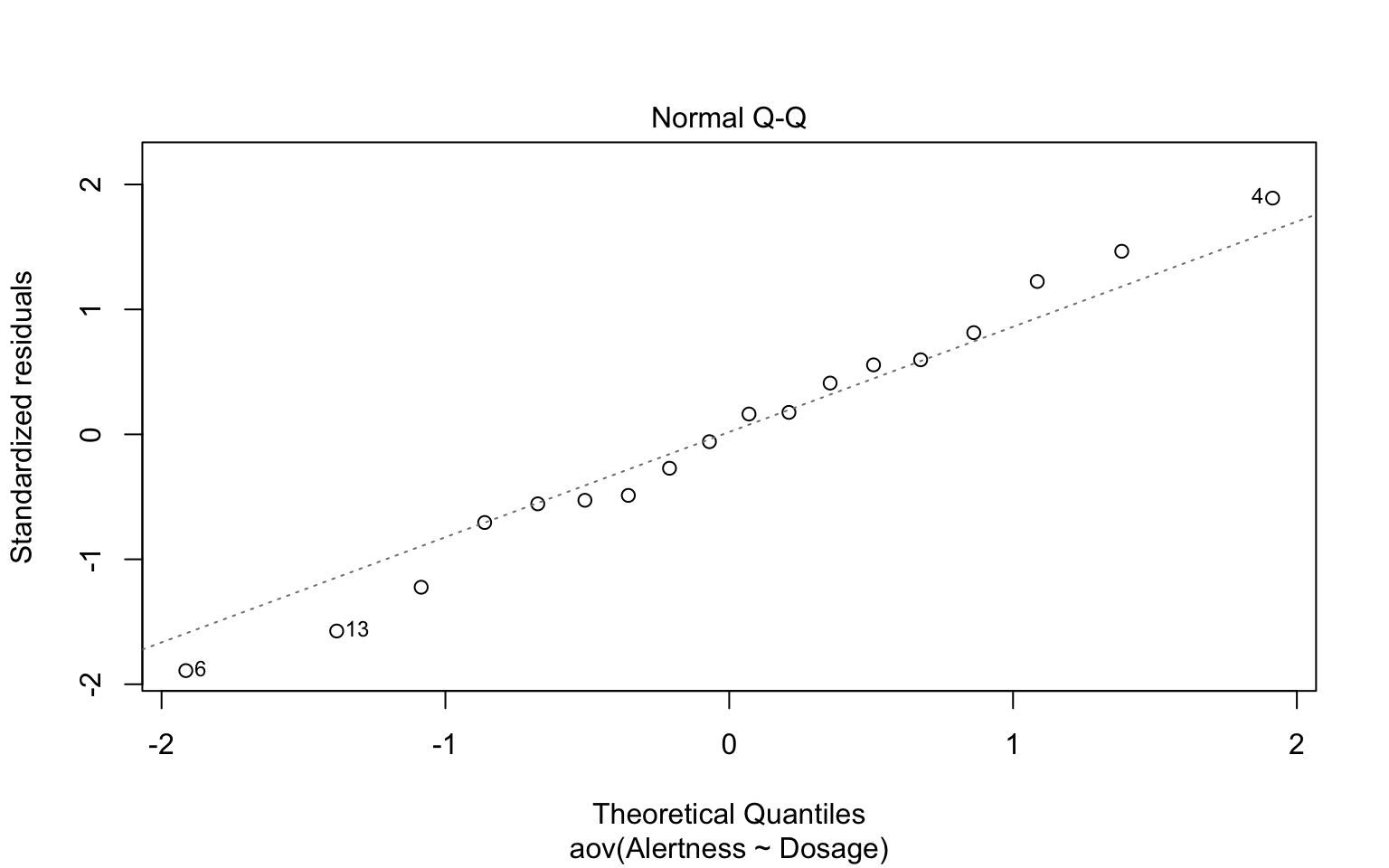
# Use plot function to get a QQ plot
plot(aov.ex1, 2)

# Run Shapiro-Wilk test
shapiro.test(x = residuals(aov.ex1))


    Shapiro-Wilk normality test

data:  residuals(aov.ex1)
W = 0.98604, p-value = 0.991

Non-parametric alternative to one-way ANOVA test: Kruskal-Wallis rank sum test

When ANOVA assumptions are not met, you cna use a non-parametric alternative.

kruskal.test(Alertness ~ Dosage, data = data1)


    Kruskal-Wallis rank sum test

data:  Alertness by Dosage
Kruskal-Wallis chi-squared = 9.4272, df = 2, p-value = 0.008972

In-Class Acitivity: Multiple pairwise-comparison

Bonferroni and Holm multiple pairwise-comparisons

In one-way Anova, a siginificant p-value means some of the group means are different. However, this does not tell us which pairs of groups are different. We can perform multiple pairwise-comparison to test the statistically significant mean difference between particular pairs of group. Given the significant ANOVA test, we can compute adjusted p-values using pairwise.t.test.

# no adjustment
pairwise.t.test(data1$Alertness, data1$Dosage, data = , p.adj = "none")


    Pairwise comparisons using t tests with pooled SD 

data:  data1$Alertness and data1$Dosage 

  a       b      
b 0.13088 -      
c 0.00082 0.00926

P value adjustment method: none

# Bonferroni
pairwise.t.test(data1$Alertness, data1$Dosage, data = , p.adj = "bonf")


    Pairwise comparisons using t tests with pooled SD 

data:  data1$Alertness and data1$Dosage 

  a      b     
b 0.3926 -     
c 0.0025 0.0278

P value adjustment method: bonferroni

# Holm
pairwise.t.test(data1$Alertness, data1$Dosage, data = , p.adj = "holm")


    Pairwise comparisons using t tests with pooled SD 

data:  data1$Alertness and data1$Dosage 

  a      b     
b 0.1309 -     
c 0.0025 0.0185

P value adjustment method: holm

Tukey multiple pairwise-comparisons

Tukey HSD (Tukey Honest Significant Differences) using TukeyHD.

# diff: difference between means of the two groups lwr, upr: the lower and
# the upper end point of the confidence interval at 95% (default) p adj:
# p-value after adjustment for the multiple comparisons.

TukeyHSD(aov.ex1)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = Alertness ~ Dosage, data = data1)

$Dosage
      diff       lwr       upr     p adj
b-a  -4.25 -11.15796  2.657961 0.2768132
c-a -13.25 -21.50659 -4.993408 0.0022342
c-b  -9.00 -16.83289 -1.167109 0.0237003

In-Class Acitivity: Planned Constrasts

You can test some specific hypotheses than testing all possible mean comparisons. We can combine multiple means from different levels and compare two means (e.g., a and b vs. c)

# assign values to the groups that you want to compare
c1 <- c(0.5, -0.5, 0)  # H0_c1: a = b
c2 <- c(0.5, 0.5, -1)  # H0_c2: a & b = c

# assign the contrasts
data1$c1 <- c(rep(0.5, 6), rep(-0.5, 8), rep(0, 4))
data1$c2 <- c(rep(0.5, 6), rep(0.5, 8), rep(-1, 4))

# compare differences between pairs of means (using regression)
anova(lm(Alertness ~ c1 + c2, data = data1))

Analysis of Variance Table

Response: Alertness
          Df Sum Sq Mean Sq F value   Pr(>F)   
c1         1  42.98   42.98  1.7722 0.202990   
c2         1 383.27  383.27 15.8051 0.001218 **
Residuals 15 363.75   24.25                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

FYI: Visualize your data using ggpubr

Bar plots with mean +/- se with jittered points

# Install R package ggpubr

## Recommended: Install the latest developmental version from GitHub (remove
## # below) if(!require(devtools)) install.packages('devtools')
## devtools::install_github('kassambara/ggpubr')

## If that failed, try one from CRAN (Remove # below)
## install.packages('ggpubr') install.packages('ggplot2')

# Load ggpubr
library(ggpubr)
library(ggplot2)

ggbarplot(data1, x = "Dosage", y = "Alertness", add = c("mean_se", "jitter"))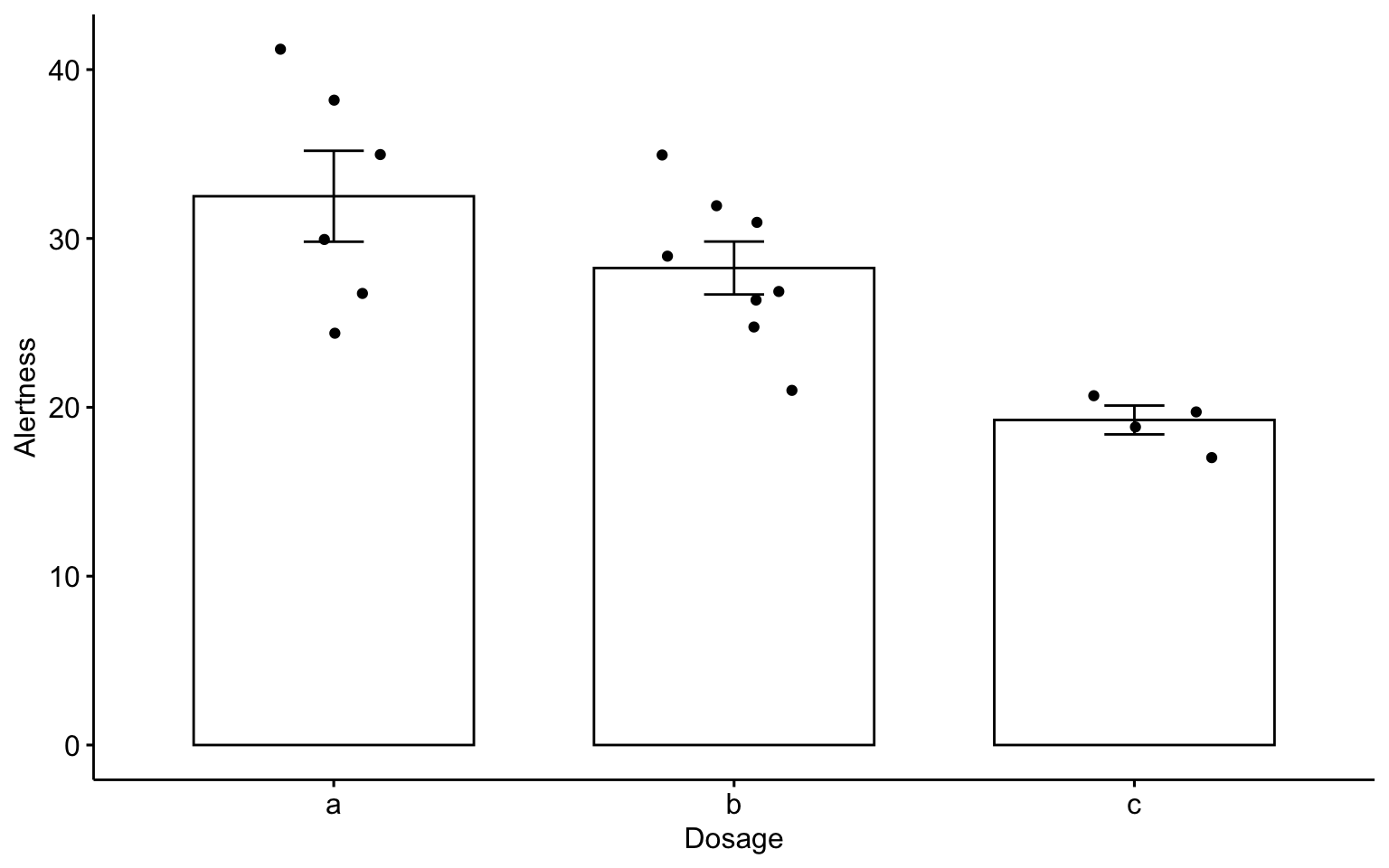

In-Class Acitivity: Tidyverse

tidyverse is an opinionated collection of R packages designed for data science. https://www.tidyverse.org/ This is designed to make it easy to install and load core packages from the tidyverse. magrittr offers a set of operators which make your code more readable such as the pipe operator %>% https://magrittr.tidyverse.org/ dplyr provides a set of tools for efficiently manipulating datasets: https://dplyr.tidyverse.org/.

# The easiest way to get dplyr or magrittr is to install the whole
# tidyverse: install.packages('tidyverse')

# Alternatively, install just dplyr or magritter: install.packages('dplyr')
# install.packages('magrittr')

library(magrittr)
library(dplyr)
library(tidyverse)

Computes summary tables using dplyr

data1 %>% group_by(Dosage) %>% summarise(count = n(), mean = mean(Alertness, 
    na.rm = TRUE), sd = sd(Alertness, na.rm = TRUE))

# A tibble: 3 x 4
  Dosage count  mean    sd
  <fct>  <int> <dbl> <dbl>
1 a          6  32.5  6.60
2 b          8  28.2  4.43
3 c          4  19.2  1.71

Assignment 10 (Week 15)

Read Data

We will use build-in data set Prestige contained in the R package car. We will load and print the survey data.

# 1. Load the required package. install.packages('car') # if you don't have
# the 'car' package, make sure to install it.
library(car)

# 2. Load the data
data(Prestige)

# 2. Print
head(Prestige)

                    education income women prestige census type
gov.administrators      13.11  12351 11.16     68.8   1113 prof
general.managers        12.26  25879  4.02     69.1   1130 prof
accountants             12.77   9271 15.70     63.4   1171 prof
purchasing.officers     11.42   8865  9.11     56.8   1175 prof
chemists                14.62   8403 11.68     73.5   2111 prof
physicists              15.64  11030  5.13     77.6   2113 prof

Check Data

Check the number of rows and columns.

# Display the internal structure of an R object.
str(Prestige)

'data.frame':   102 obs. of  6 variables:
 $ education: num  13.1 12.3 12.8 11.4 14.6 ...
 $ income   : int  12351 25879 9271 8865 8403 11030 8258 14163 11377 11023 ...
 $ women    : num  11.16 4.02 15.7 9.11 11.68 ...
 $ prestige : num  68.8 69.1 63.4 56.8 73.5 77.6 72.6 78.1 73.1 68.8 ...
 $ census   : int  1113 1130 1171 1175 2111 2113 2133 2141 2143 2153 ...
 $ type     : Factor w/ 3 levels "bc","prof","wc": 2 2 2 2 2 2 2 2 2 2 ...

# Check the dimension of an object
dim(Prestige)

[1] 102   6

Use the help function to learn about variables

If you want to learn more about the t.test function.

# A question mark is a shorcut for the 'help' function.
`?`(Prestige)

HD 5514 Research Methods (Fall 2019)

Analysis of Variance (W15)

HD 5514 Research Methods (Fall 2019)

In-Class Acitivity: Analysis of Variance (ANOVA)

Load Data

Check Data Set

Visualize your data - Boxplot & Histogram

Conduct one-way Anova

Report means

Check ANOVA assumptions

Check the homogeneity of variance assumption: Levene’s test

ANOVA test with no assumption of equal variances: Welch one-way test

Check the normality assumption

Non-parametric alternative to one-way ANOVA test: Kruskal-Wallis rank sum test

In-Class Acitivity: Multiple pairwise-comparison

Bonferroni and Holm multiple pairwise-comparisons

Tukey multiple pairwise-comparisons

In-Class Acitivity: Planned Constrasts

FYI: Visualize your data using ggpubr

Bar plots with mean +/- se with jittered points

In-Class Acitivity: Tidyverse

Computes summary tables using dplyr

Assignment 10 (Week 15)

Read Data

Check Data

Use the help function to learn about variables