Load Data

We are going to use mtcars data included in R by default. We will load and print the mtcars data.

# 1. Loading
data(mtcars) 

# 2. Print
head(mtcars)

Print Data

We can view the content of the mtcars data.

# 2. Print (the first 6 rows)
head(mtcars)

# Print the last 6 rows
tail(mtcars)

# Print the first 10 rows
head(mtcars, 10)

Check Data Set

Check the number of rows and columns.

# Display the internal structure of an R object.
str(mtcars)

# Check the dimension of an object
dim(mtcars)

# Number of rows (observations)
nrow(mtcars)

# Number of columns (variables)
ncol(mtcars)

If you want to learn more about the mtcars data set, you can bring up a helpful file for functions and datsets.

# Bring up a help file
help(mtcars) 

# A question mark is a shorcut for the "help" function.
?mtcars

Check the data frame column (mpg)

First, find the data column, named mpg (gas mileage) of the mtcars data set.

# Print the mpg column
mtcars$mpg

# Create a freqeuncy table for the mpg column
table(mtcars$mpg)

# Compute mean
mean(mtcars$mpg)

# Compute standard deviation
sd(mtcars$mpg)

# Statistical summaries of mpg
summary(mtcars$mpg)

Visualize your data using a box plot

First, find the data column, named mpg (gas mileage) of the mtcars data set.

# Create a box plot
#par(mar=c(1,1,1,1))
boxplot(mtcars$mpg)

# Add axes and text
boxplot(mtcars$mpg,
data=airquality,
main="Car Milage Data",
xlab="Gas mileage",
ylab="Miles/(US) gallon",
col="orange",
border="brown"
)

Compute one-sample t-test (two.sided)

Use the t.test() function to perfom one-sample t-test (two.sided)

# two-tailed test
t.test(mtcars$mpg, mu = 0, alternative = "two.sided")

# < 2.2e-16 is equal to 2.2 x 10^-16, 0.00000000000000022 with 15 zeros after the decimal point (E: scientific (or exponential) notation, 10 to the x-th power)

Compute one-sample t-test (one.sided)

Using the alternative argument to change the alternative hypothesis. alternative argument allows one of the following options: “two.sided” (default), “greater” or “less”.

# one-tailed test
t.test(mtcars$mpg, mu = 0, alternative = "less")

# one-tailed test
t.test(mtcars$mpg, mu = 0, alternative = "greater")

Compute one-sample t-test with a different mean

Using the mu argument to change the theoretical mean. Default is 18 but you can change it (mu = 20).

# two-tailed test
t.test(mtcars$mpg, mu = 18, alternative = "two.sided")

# one-tailed test (greater)
t.test(mtcars$mpg, mu = 18, alternative = "greater")

Use the help function

If you want to learn more about the t.test function.

# A question mark is a shorcut for the "help" function.
?t.test

Check two data frame columns (mpg, am)

If two samples come from unrelated populations, they are independent.

First, find the data column, named mpg (gas mileage) of the mtcars data set.

# Print the mpg column
mtcars$mpg

# Create a freqeuncy table for the mpg column
table(mtcars$mpg)

# Compute mean
mean(mtcars$mpg)

# Compute standard deviation
sd(mtcars$mpg)

Next, find another data column, named am (transmission type; 0 = automatic, 1 = manual) in the mtcars data set.

# Print the am column
mtcars$am

# Create a freqeuncy table for the am column
table(mtcars$am)

Conduct the unpaired t-test between two populations means

If two samples come from unrelated populations, they are independent. Compute the difference in means of the two sample data using the t.test fuction

# Method 1
t.test(mtcars$mpg, mtcars$am)

# Method 2 (model response variable mpg by the predictor am)
t.test(mtcars$mpg ~ mtcars$am)

# Welch Two Sample t-test is more reliable when the two samples have unequal variances and/or unequal sample size.

Read Data

We will use build-in data set sleep. We will load and print the survey data.

# 1. Loading
data(sleep) 

# 2. Print
head(sleep)

Check Data

Check the number of rows and columns.

# Display the internal structure of an R object.
str(sleep)

# Check the dimension of an object
dim(sleep)

Use the help function to learn about variables

If you want to learn more about the t.test function.

# A question mark is a shorcut for the "help" function.
?sleep

Check two data frame columns (group, extra)

First, find the data column, named extra, of the survey data set.

# Summary of the "extra" column
summary(sleep$extra)

Next, find another data column, named group in the survey data set.

# Summary of the "group" column
summary(sleep$group)

# Create a freqeuncy table for the "group" column
table(sleep$group)

Conduct the unpaired t-test between two populations means (Welch t-test by default)

Compute the difference in means of the two sample data using the t.test fuction. By default, t.test does not assume equal variances; instead of Student’s t-test, it uses the Welch t-test by default.

# Method 1 (Do not use Method 1 for Assignment #8)
#t.test(sleep$extra, sleep$group)

# Method 2 (Use Method 2 for Assignment #8)
t.test(sleep$extra ~ sleep$group)

Conduct the unpaired t-test between two populations means (Student’s t-test)

Now, assume equal variance and use Student’s t-test by setting var.equal=TRUE.

# Conduct Student t-test
t.test(sleep$extra ~ sleep$group, sleep, var.equal=TRUE)

FYI: Test equal variance using Bartlett’s test

You can test whether two or more samples are drawn from populations with “equal variance” using Bartlett’s test. The null hypothesis of this test is that the variances are equal. The alterntive hypothesis is that they are not equal. If you fail to reject the null hypothesis, that means there is not enough evidence to suggest that the variance is different for groups. Thus, you can assume equal variance.

# Conduct Bartlett’s test with the bartlett.test function
bartlett.test(sleep$extra~sleep$group)

FYI: Visualize your data using a box plot by group

You can visualize both groups (1 and 2) using the boxplot function.

boxplot(sleep$extra ~ sleep$group)

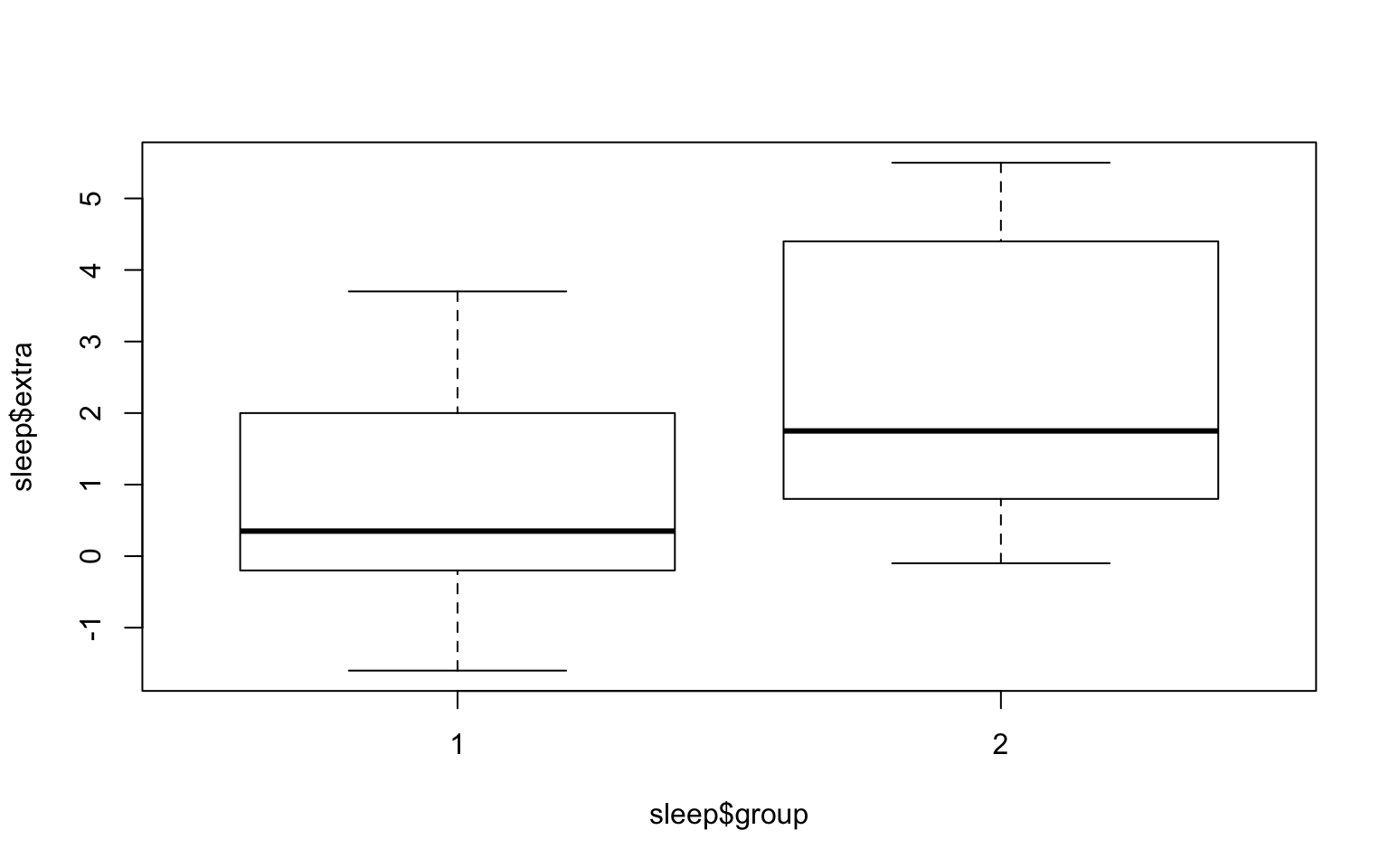
FYI: Conduct the paired t-test

When each subject is measured twice such as repeated-measures designs, it will result in pairs of observations that are not independent. In this case, we analyze the differences before and after using a paird sample t-test. We will test whether the mean values for the extra variable differs by the group variable to look at the difference between the two groups (group 1 and group 2).

t.test(extra ~ group, data = sleep, paired = TRUE)

    Paired t-test

data:  extra by group
t = -4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -2.4598858 -0.7001142
sample estimates:
mean of the differences 
                  -1.58